Quantitative magnetization transfer using spoiled gradient echo

Magnetization Transfer (MT) has been extensively applied to study macromolecular biological tissue composition. The imaging contrast resides in the magnetization transfer between free-water protons and macromolecular proton compartments, through chemical exchange and dipolar interactions. In the two-pool tissue model, highly mobile protons are associated with the free-water pool while protons found in semisolid macromolecular sites are defined as the restricted pool (Sled 2018). A simple method for visualizing MT effects includes acquiring two images with and without an off-resonance MT pulse to calculate the MT ratio (MTR), which is the normalized difference of these two images (Wolff and Balaban 1989). Despite its proven usefulness to study multiple sclerosis (Zheng et al. 2018), Alzheimer’s disease (Fornari et al. 2012) and psychiatric disorders (Chen et al. 2015), the MTR is a semi-quantitative metric that depends critically on the imaging sequence parameters (Wood and Malik 2020). Another semi-quantitative approach is the estimation of MT saturation (MTsat) by fitting the MT signal obtained from an MT-weighted (MTw), a proton density (PD) weighted and T₁-weighted (T₁w) contrast (Helms et al. 2008). Quantitative MT (qMT) consists of fitting multiple images to a mathematical model to extract tissue-specific parameters related to physical quantities, such as pool sizes, magnetization exchange rates between pools, and T₁,T₂ relaxation times of each pool. Compared to semi-quantitative approaches (MTR, MTsat), qMT has long acquisition protocols and sometimes needs additional measurements (eg. B₀, B₁, T₁), and the complex models required to fit the quantitative maps makes it a challenging imaging technique.

In 2015, our lab published qMTLab (Cabana et al. 2015), an open-source software project seeking to unify three qMT methods in the same interface: qMT using spoiled gradient echo (qMT-SPGR), qMT using balanced steady-state free precession (qMT-bSSFP), and qMT using selective inversion recovery with fast spin echo (qMT-SIRFSE). qMTLab allowed users to simulate, evaluate, fit, and visualize qMT data with the possibility to share qMT protocols between researchers, allowing them to compare the performance of their methods (Cabana et al. 2015). Since then, we have extended the project and renamed it to qMRLab, (Karakuzu et al. 2020), which in addition to qMT now provides over 20 quantitative techniques under one umbrella, such as relaxation and diffusion models, quantitative susceptibility mapping, B₀ and B₁ mapping. In addition, we created interactive tutorials (Boudreau 2018a; Boudreau 2018b; Boudreau 2019) and blog posts for several qMRI techniques that were published under a creative commons license, and one of these tutorials (Boudreau 2018a) made it into a quantitative MRI book published by Elsevier (Seiberlich et al. 2020). This blog post is a continuation of our qMRLab outreach initiative, where we will focus on qMT and the tools we provide in qMRLab for this class of techniques.

Below is an introduction to qMT (with a focus on qMT-SPGR), where we will cover signal modelling and data fitting.

Signal Modelling

The magnetization transfer in a two-pool model is modelled by a set of coupled differential equations (Sled and Pike 2000):

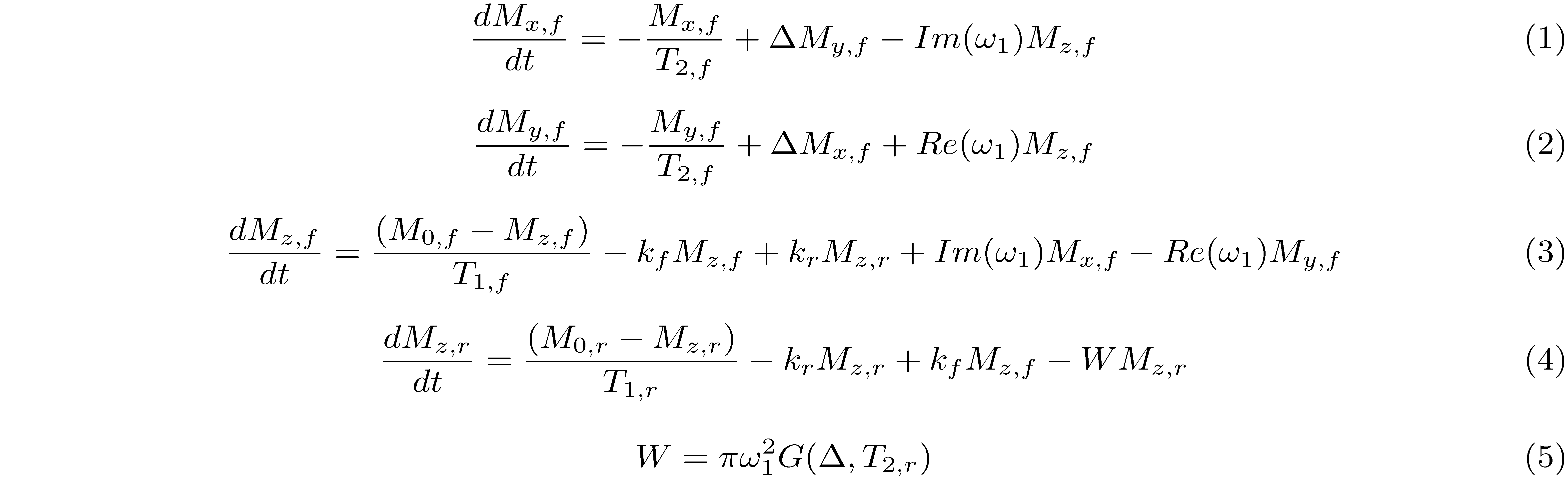
where the magnetization at time $t$ is given by M = [M_x,f, M_y,f, M_z,f, M_z,r] and M_x,f and M_y,f are the transverse magnetization for the free pool in the $x$ and $y$ direction, respectively. The longitudinal magnetization for the free and restricted pool is denoted by M_z,f and M_z,r. Due to the very short T₂ of the restricted pool (on the order of microseconds), the transverse magnetization of this pool is not explicitly modelled.

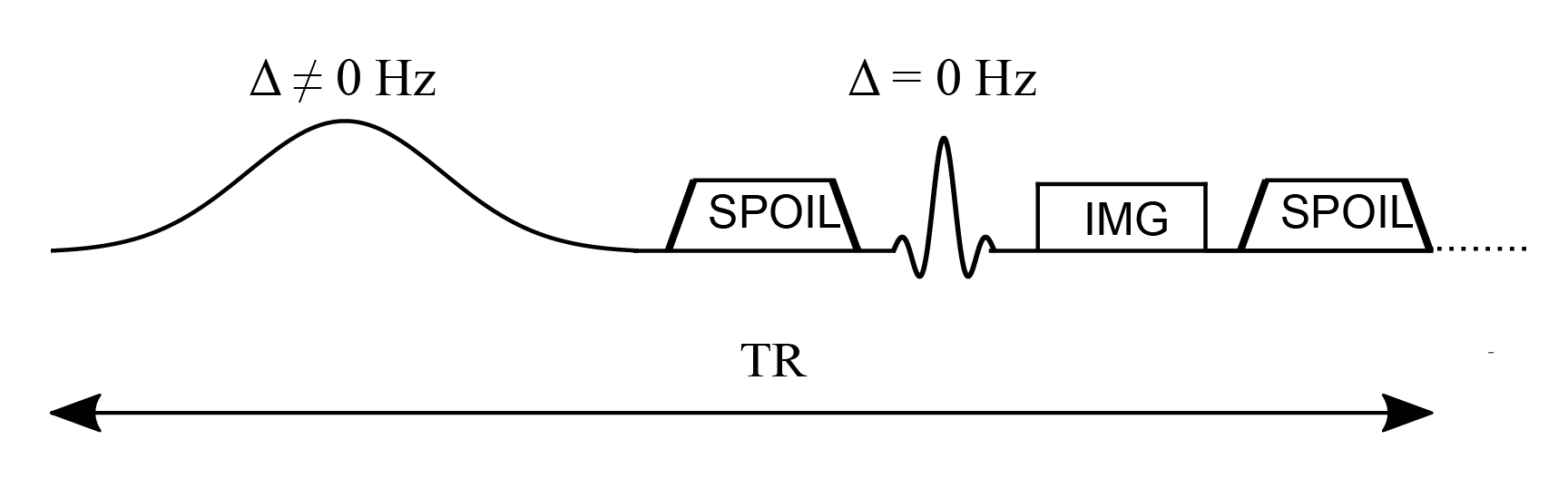
The constants k_f and k_r represent the exchange rate of the longitudinal magnetization from the free pool to the restricted pool (k_f) and from the restricted to the free pool (k_r). The ratio of these quantities is constrained by the size of the restricted to the free-water pool, expressed as k_f/k_r = M_0,r/M_0,f. This ratio is called the pool size ratio $F$ defined as F = M_0,r/M_0,f. The precessional frequency ω₁ is a measure of the power of the off-resonance radiofrequency pulse and ∆ is a frequency offset at which the magnetic B₁⁺ field is applied. As shown in Figure 1, an on-resonance (∆ = 0) radiofrequency pulse is also part of the pulse sequence and is applied after the MT pulse. The relaxation time constants for the free and restricted pools are denoted by T_1,f and T_1,r for the longitudinal magnetization, and T_2,f and T_2,r for the transverse magnetization. Finally, $W$ is the saturation rate of the restricted pool, which is a function of the absorption lineshape $G$ that depends on the frequency offset and the transverse relaxation of the restricted pool (Figure 2).

Figure 1. Simplified pulse sequence diagram of a magnetization transfer spoiled gradient (MT-SPGR) experiment with an MT pulse followed by a spoiler gradient to destroy any transverse magnetization before the application of the on-resonance excitation pulse.

The absorption lineshape of the restricted pool that best characterizes the proton system depends on the environment. For simple systems such as agar gel phantoms, the Gaussian lineshape describes magnetization transfer effects well (Hankelman et al. 1993), while for more complicated and biologically relevant models, the super-Lorentzian lineshape is the best choice (Morrison et al. 1995).

Figure 2. Gaussian, Lorentzian and super-Lorentzian absorption lineshapes plotted as a function of the frequency offset ∆ and T_2,r.

In a standard qMT experiment, multiple measurements are required where the off-resonance radiofrequency pulse angle (MT angle) and offset frequency are changed for each measurement, and at least one measurement is acquired in the absence of an MT pulse. The acquired signal plotted as a function of the the offset frequency is known as the “Z-spectrum”, and Figure 3 shows the Z-spectrum simulated using different absorption lineshapes. The off-resonance MT pulse is modelled either as a continuous wave or as a pulsed irradiation scheme. In a continuous wave irradiation mode, long off-resonance pulses of constant saturation and fixed frequency offset are applied to generate well-defined MT states in the two pools (Henkelman et al. 2001). For more practical implementations, pulsed off-resonance irradiations are used with a spoiled gradient echo sequence (SPGR) to generate MT-weighted images at different saturation rates and frequency offsets (Sled and Pike 2000). In the qMT-SPGR sequence shown in Figure 1, the MT preparation pulse is applied, followed by a spoiler gradient to eliminate any residual transverse magnetization produced by the long MT pulses, and to destroy the MR signal from previous measurements. A signal equation for this type of pulsed MT experiment can be derived by approximating the pulse sequence to a series of stages described by a continuous wave off-resonance irradiation period, followed by free precession, and instant saturation of the free-water pool (Cabana et al. 2015; Sled and Pike 2000; Sled and Pike 2001). This pulse sequence decomposition allows for analytically solving the Bloch-McConnell equations at a steady-state, but it is also possible to numerically solve the Bloch equations to perform simulations that provide a more realistic approximation when the system has not been driven to a steady-state. A comparison between the Bloch simulations and the analytical solution is shown in Figure 4 for different numbers of preparation MT pulses. As can be seen, different frequency offsets and MT flip angles require different numbers of repetition times to reach the steady-state, which is of paramount importance since the analytical solution used for parameter estimation is derived assuming the steady-state. In terms of data acquisition optimization, the k-space periphery is sampled during the preparation pulses whereas the center of k-space, that contains the overall image contrast, is acquired once the steady-state is achieved.

Figure 3. Z-spectrum simulated using different absorption lineshapes (Gaussian, Lorentzian, and super-Lorentzian).

Figure 4. Z-spectrum simulated using Bloch simulations (dashed lines) for a number of MT pulses ranging from 1 to 600. Bloch simulations are compared with the Z-spectrum obtained from the analytical solution (solid lines).

Data Fitting

In qMT imaging, the biophysical model relates the parameters observed in the two-pool tissue model to physical quantities such as the fractional size of the pools, relaxation times and magnetization exchange rates of the free and restricted pool (Sled and Pike 2001; Sled 2018). However, qMT experiments usually consist of long acquisition imaging protocols accompanied by complex data fitting. To this end, some software solutions have been proposed (Karakuzu et al. 2020; Tabelow et al. 2019; Wood 2018). qMRLab is an open-source project for quantitative MR analysis that is an extension of qMTLab, a software for data simulation and analysis of three MT models: qMT-SPGR, qMT-bSSFP and qMT-SIRFSE. In addition to the quantitative MT methods, qMRLab also contains semi-quantitative MT models including the magnetization transfer ratio (MTR) and magnetization transfer saturation (MTsat).

The qMT-SPGR method in qMRLab contains three fitting models: Sled and Pike, Ramani, and Yarnykh and Yuan (Sled and Pike 2001; Ramani et al. 2002; Yarnykh 2002). For the Sled and Pike model, the saturation fraction effect of the MT pulse on the free pool is pre-computed to accelerate the processing times. The MT effect of the pulse is approximated as an instantaneous fractional saturation of the longitudinal magnetization of the free pool, assuming the absence of chemical exchange processes (Pike 1996; Sled and Pike 2001). To fit the model, additional parameters related to the pulse sequence are required, namely timing parameters, the absorption lineshape, and the characteristics of the MT pulse, such as the shape and the bandwidth or the time-bandwidth product. In Figure 5, the qMT-SPGR method is used to show a single voxel curve simulation for the same MT data fitted by three different models. The fitted parameters were the pool size ratio F, the magnetization transfer rate from the restricted to the free-water pool (k_r), and the transverse relaxation time of the free-water (T_2,f) and restricted (T_2,r) pool.

Figure 5. Sled and Pike, Ramani, and Yarnykh and Yuan models to fit the MT data from a qMT-SPGR experiment.

In addition to acquiring the MT data, three more quantitative measurements are typically required for model correction purposes. The magnetic field B₀ inhomogeneity affects the actual off-resonance frequency experienced by the tissue at each voxel. In MT, B₀ maps are computed to correct for off-resonance frequency values of the MT pulse in the presence of magnetic field non-uniformity. Radiofrequency field B₁ inhomogeneity is another source of inaccuracies that depend on the operating frequency of the scanner, the pulse sequence, and the shape and electrical properties of the sample (Sled and Pike 1998). Therefore, B₁ maps are typically needed to correct the radiofrequency amplitude variations that affect the nominal values of the MT pulse flip angle and the excitation flip angle (Boudreau et al. 2018c). Longitudinal relaxation T₁ values vary naturally in biological tissue, but the choice of the T₁ mapping method, has also been shown to influence the variability of T₁ measurements (Stikov et al. 2015). In the context of a qMT experiment, T₁ maps are acquired with an independent measurement of the apparent relaxation time T₁ (T₁^meas). The T₁ map is related to the relaxation rate of the free pool (R_1,f) as described by equation 6, expressed in terms of $F$, k_f, R₁^meas and R_1,r, where the relaxation rate of the restricted pool is arbitrarily set to 1 s^-1 because it is insensitive to this kind of MT experiments (Sled and Pike 2001). Multiple qMRI maps with a range of B₀ and B₁ inaccuracies, as well as T₁ maps with a variety of relaxation times, have been simulated to show the effect of the quality of these input maps on the qMT fitted parameters as shown in Figure 6.

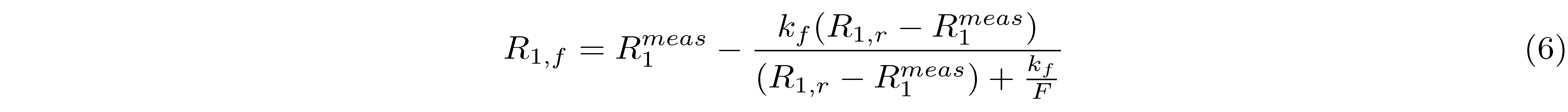
Figure 6. Errors (%) in fitted parameters when input maps of different quality are used. A B₁ map of 0.9 means that the input has a 10% lower value than expected. The fitted parameters include the pool size ratio, F, the magnetization exchange rate, k_f, the free pool T_2,f, and the restricted pool T_2,r. The errors were simulated for B₀, B₁ and T₁ maps of different quality.

As described above in Figure 6, inaccurate MT pulse flip angles and excitation flip angles affect the fitted MT parameters, and there is an additional error source related to the T₁ mapping measurement. As Boudreau et al. (2018c) have shown, using specific acquisitions protocols, T₁ values can be affected by B₁ field non-uniformities, such as the variable flip angle method, while the inversion recovery method is insensitive to these field inhomogeneities (Stikov et al. 2015).

Figure 7 displays an example human dataset with the input qMRI maps used to fit the qMT parameters F, k_f, T_2,f, T_2,r.

Figure 7. Example magnetization transfer spoiled gradient dataset showing qMRI maps used to fit the MT data (top), and the fitted parameters F, k_f, T_2,f, T_2,r (bottom).

Summary

In summary, the Bloch-McConnell equations, an analytical solution to the steady-state signal can be derived and fitted with one of the existing models that make different approximations to fit the qMT data for a different set of parameters. The Sled and Pike model (2001) constrains the solution space by computing complementary T₁ maps, whose acquisition method influences the B₁ sensitivity of the fitted parameters (Boudreau et al. 2018c). This fitting model can be implemented with a continuous or a rectangular wave irradiation of the restricted pool (Cabana et al. 2015). Ramani’s fitting model is an alternative approach that assumes a continuous wave irradiation scheme with the MT pulse on both free and restricted pools (Ramani et al. 2002). Another fitting model was proposed by Yarnykh (2002) where an analytical solution to describe the magnetization is found when the direct saturation of the free pool is neglected.

In future blog posts, we will explore other MT methods, such as MTR (Wolff and Balaban 1989), MTsat (Helms et al. 2008) and qMT-bSSFP (Brieri and Scheffler 2007; Gloor et al. 2008). Additionally, we will also be looking at the effects of RF field inhomogeneity on the generated magnetization transfer maps.

Works Cited

Bieri, O. & Scheffler, K., 2007. Optimized balanced steady-state free precession magnetization transfer imaging. Magn. Reson. Med., 58, pp.511-518. https://doi.org/10.1002/mrm.21326

Boudreau, M. (2018a, October 23). Relaxometry series: Inversion recovery. qMRLab. Retrieved April 26, 2022, from https://qmrlab.org/jekyll/2018/10/23/T1-mapping-inversion-recovery.html

Boudreau, M. (2018b, December 11). Relaxometry series: Variable flip angle. qMRLab. Retrieved April 26, 2022, from https://qmrlab.org/jekyll/2018/12/11/T1-mapping-variable-flip-angle.html

Boudreau, M., Stikov, N. & Pike, G.B, 2018c. B1-sensitivity analysis of quantitative magnetization transfer imaging. Magn. Reson. Med., 79, pp.276-285. https://doi.org/10.1002/mrm.26673

Boudreau, M. (2019, April 08). Relaxometry series: MP2RAGE. qMRLab. Retrieved April 26, 2022, from https://qmrlab.org/2019/04/08/T1-mapping-mp2rage.html

Cabana, J.-F., Gu, Y., Boudreau, M., Levesque, I.R., Atchia, Y., Sled, J.G., Narayanan, S., Arnold, D.L., Pike, G.B., Cohen-Adad, J., Duval, T., Vuong, M.-T. & Stikov, N., 2015. Quantitative magnetization transfer imaging made easy with qMTLab: Software for data simulation, analysis, and visualization. Concepts Magn. Reson., 44A, pp.263-277. https://doi.org/10.1002/cmr.a.21357

Chen, Z., Zhang, H., Jia, Z., Zhong, J., Huang, X., Du, M., Chen, L., Kuang, W., Sweeney, J.A. & Gong, Q., 2015. Magnetization Transfer Imaging of Suicidal Patients with Major Depressive Disorder. Sci. Rep., 5, 9670. https://doi.org/10.1038/srep09670

Fornari, E., Maeder, P., Meuli, R., Ghika, J. & Knyazeva, M.G., 2012. Demyelination of superficial white matter in early Alzheimer's disease: a magnetization transfer imaging study. Neurobiol. Aging., 33(2), pp.428.e7-19. https://doi.org/10.1016/j.neurobiolaging.2010.11.014

Gloor, M., Scheffler, K. & Bieri, O., 2008. Quantitative magnetization transfer imaging using balanced SSFP. Magn. Reson. Med., 60, pp.691-700. https://doi.org/10.1002/mrm.21705

Helms, G., Dathe, H., Kallenberg, K. & Dechent, P., 2008. High-resolution maps of magnetization transfer with inherent correction for RF inhomogeneity and T1 relaxation obtained from 3D FLASH MRI. Magn. Reson. Med., 60, pp.1396-1407. https://doi.org/10.1002/mrm.21732

Henkelman, R.M., Huang, X., Xiang, Q.-S., Stanisz, G.J., Swanson, S.D. & Bronskill, M.J., 1993. Quantitative interpretation of magnetization transfer. Magn. Reson. Med., 29, pp.759-766. https://doi.org/10.1002/mrm.1910290607

Henkelman, R.M., Stanisz, G.J. & Graham, S.J., 2001. Magnetization transfer in MRI: a review. NMR Biomed., 14, pp.57-64. https://doi.org/10.1002/nbm.683

Karakuzu, A., Boudreau, M., Duval, T.,Boshkovski, T., Leppert, I.R., Cabana, J.F., Gagnon, I., Beliveau, P., Pike, G.B., Cohen-Adad, J. & Stikov, N., 2020. qMRLab: Quantitative MRI analysis, under one umbrella. Journal of Open Source Software, 5(53), 2343 https://doi.org/10.21105/joss.02343

Morrison, C., Stanisz, G. & Henkelman, R.M., 1995. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J. Magn. Reson. B., 108(2), pp.103–113. https://doi.org/10.1006/jmrb.1995.1111

Pike, G.B., 1996. Pulsed magnetization transfer contrast in gradient echo imaging: a two-pool analytic description of signal response. Magn. Reson. Med., 36(1), pp.95-103. https://doi.org/10.1002/mrm.1910360117

Ramani, A., Dalton, C., Miller, D.H., Tofts, P.S. & Barker, G.J., 2002. Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn. Reson. Imaging., 20(10), pp.721-731. https://doi.org/10.1016/s0730-725x(02)00598-2

Seiberlich, N., Gulani, V., Campbell, A., Sourbron, S., Ivanova Doneva, M., Calamante, F. & Hu, H.H., (Eds.), 2020. Quantitative magnetic resonance imaging (1st Ed.). Elsevier.

Sled, J.G. & Pike, G.B., 1998. Standing-wave and RF penetration artifacts caused by elliptic geometry: an electrodynamic analysis of MRI. IEEE Trans. Med. Imaging., 17(4), pp.653-662. https://doi.org/10.1109/42.730409

Sled, J.G., & Pike, G.B., 2000. Quantitative Interpretation of Magnetization Transfer in Spoiled Gradient Echo MRI Sequences. Journal of Magnetic Resonance., 145(1), pp.24-36. https://doi.org/10.1006/jmre.2000.2059

Sled, J.G. & Pike, G.B., 2001. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn. Reson. Med., 46, pp.923-931. https://doi.org/10.1002/mrm.1278

Stikov, N., Boudreau, M., Levesque, I.R., Tardif, C.L., Barral, J.K. & Pike, G.B., 2015. On the accuracy of T1 mapping: Searching for common ground. Magn. Reson. Med., 73, pp.514-522. https://doi.org/10.1002/mrm.25135

Tabelow, K., Balteau, E., Ashburner, J., Callaghan, M.F., Draganski, B., Helms, G., Kherif, F., Leutritz, T., Lutti, A., Phillips, C., Reimer, E., Ruthotto, L., Seif, M., Weiskopf, N., Ziegler, G. & Mohammadi, S., (2019). hMRI - A toolbox for quantitative MRI in neuroscience and clinical research. Neuroimage., 194, pp.191-210. https://doi.org/10.1016/j.neuroimage.2019.01.029

Wolff, S.D. and Balaban, R.S., (1989), Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn. Reson. Med., 10, pp.135-144. https://doi.org/10.1002/mrm.1910100113

Wood, (2018). QUIT: QUantitative Imaging Tools. Journal of Open Source Software, 3(26), 656. https://doi.org/10.21105/joss.00656

Wood, T.C. & Malik, S.J., 2020. Magnetization transfer. In N. Seiberlich, V. Gulani, A. Campbell, S. Sourbron, M. I. Doneva, F. Calamante & H. H. Hu (Eds.), Quantitative Magnetic Resonance Imaging, Volume 1. (1st ed, pp.47-64). Elsevier.

Yarnykh, V.L., 2002. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: Theory and clinical applications. Magn. Reson. Med., 47, pp.929-939. https://doi.org/10.1002/mrm.10120

Yarnykh, V.L., 2012. Fast macromolecular proton fraction mapping from a single off-resonance magnetization transfer measurement. Magn. Reson. Med., 68, pp.166-178. https://doi.org/10.1002/mrm.23224

Zheng, Y., Lee, J.-C., Rudick, R. & Fisher, E., 2018. Long-Term Magnetization Transfer Ratio Evolution in Multiple Sclerosis White Matter Lesions. Journal of Neuroimaging, 28, pp.191-198. https://doi.org/10.1111/jon.12480